ML Geek

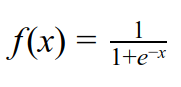
I've been exploring some very common activation functions and visualizing what effects these activation functions bring to the output at each layer. Before we dive into some details, let me first introduce these activation functions. I. Activation functions 1. Sigmoid Sigmoid is one of the most common activation functions. The output of sigmoid can be interpreted as "probability" since it squashes the values to the range (0,1) so it is very intuitive to use sigmoid at the last layer of a network (before classifying). Sigmoid function takes on the form Sigmoid is a smooth function and is differentiable; however it suffers from gradient saturation issue when x  is very large or very small (i.e. the gradient is very small). As depicted in the figure below, when f  approaches either 0  or 1, the gradient becomes very small. Another issue of the sigmoid function is that the output of it is not zero-centered. Therefore, in many cases tanh is preferred. 2. Tanh

I recently came across Tom Mitchell's comparison of Naive Bayes and Logistic Regression. Under some specific assumptions, Naive Bayes can be interpreted in terms of Logistic Regression. Furthermore, as the number of training examples reach infinity, under the aforementioned constraint, NB and LR classifiers are identical. In this blog I'll explain the bias of Naive Bayes, including the reason why using Naive Bayes instead of unbiased learning of Bayes classifiers, along with the relationship between Naive Bayes and Logistic Regression. 1. Why Naive Bayes? Consider the unbiased learning of Bayes classifiers. Given a supervised learning problem, we want to estimate a function f that maps input X  to output Y , f : X -> Y , or in other words, P(Y | X), where X  is the vector of n  attributes and Y  can take on k classes. Applying Bayes rule, we have the following: Since X  is a vector of n  attributes. Let's assume each attribute takes on either 0  or 1 . To represe

I've been using some of the loss functions in machine learning like Least Squared Error, Logistic Loss, Softmax Loss, etc. for quite some time but never had I dug deep into them to really understand how they were derived and the motivation behind them. Recently I took a look at Stanford's CS 229 materials and find it mind-blowing to finally have some understanding about those common loss functions and I want to share some of my knowledge here. First let's take a look at Least Squared Error. Least-squared cost function is usually used in regression problems, defined by the formula where h  is our hypothesis function of the input x  that estimates the output  y and least-squared cost function is to measure how close we are in our estimation. Clearly, the higher L the further we are from estimating y  correctly, so we are trying to minimize this cost function. But why least-squared cost function is a natural cost function to use in this case? Let's first assume that